فرمول زیبا

ریاضیدادنان غالباً مسابقاتی برای زیباترین فرمول جهان ترتیب میدهند. مقام اول، تقریباً هر بار، به فرمول کشفشده توسط لئونهارد ایلر[1] تعلق میگیرد. این فرمول در زیر ارائه شده است.![]()
این فرمول استثنائی است، چرا که ترکیبی از پنج تا از مهمترین ثابتهای ریاضی است، یعنی:
۰: عضو همانی جمع
۱: عضو همانی ضرب
π: شاه هندسه و مثلثات
i: شاه جبر پیچیده
e: شاه لگاریتمها
نحوهی پیونددادن این ثابتهای اساسی ریاضی توسط فرمولی ساده صرفاً زیباست. زمانیکه این فرمول ایلر را در دبیرستان یاد گرفتم، مدهوش شدم و هنوز هم هستم. ایلر ابداعکنندهی سمبل e (شاه لگاریتم)، که گاهاً با عنوان ثابت ایلر شناخته میشود هم هست. نامگذاری این ثابت به دلیل دیگری هم بهجا است: ایلر به پرکارترین ریاضیدان تمامی دورانها معروف است. او ریاضیات نوین را با نرخی نمایی خلق میکرد. این امر خصوصاً وقتی تکاندهنده است که بدانیم ایلر نصف عمرش تا حدودی نابینا بود و دو دههی پایانی عمر هم کاملاً نابینا شد. ازقضا، او در مدت یک هفتهی چشمگیر، یعنی زمانیکه کاملاً نابینا بود، داشت روی مقالهی علمی با کیفیت بسیار بالایی کار میکرد.
امروز، پیش از بازکردن بحث رگرسیون لجستیک، باید به این مرد بزرگ، لئونهارد ایلر ادای احترام کنیم، چرا که ثابت ایلر (e) هستهی رگرسیون لجستیک را شکل میدهد.
مثال مطالعهی موردی – بانکداری
در دو مقالهی قبلی دایکه (بخش ۱ و بخش ۲)، بهعنوان مدیر ارشد ریسک (CRO) بانک سیندیکت ایفای نقش میکردید. این بانک ۶۰۸۱۶ وام خودرو در سهماههی بین آوریل-ژوئن ۲۰۱۲ اعطا کرده بود. بهعلاوه، متوجه نرخ بد حدود ۲.۵ درصدی شدید. با استفاده از ابزارهای تصویرسازی دادهها، تعدادی تحلیل کاوشگرانهی داده (EDA) انجام دادید و رابطهای بین سن (بخش ۱) و FOIR (بخش ۲) با نرخهای بد پیدا کردید. حالا، میخواهید مدل رگرسیون لجستیک سادهای با متغیر سن بسازید. اگر یادتان باشد، هیستوگرام نرمال زیر را برای سن همپوشیشده با نرخهای بد مشاهده کردید.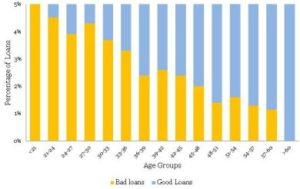
از این نمودار برای خلق دستههای نادقیقی (زمخت) بهمنظور اجرای رگرسیون لجستیک ساده استفاده خواهیم کرد. هرچند، هدف در اینجا، شناخت تفاوتهای جزئی رگرسیون لجستیک است. بنابراین، بگذارید اول برخی از مفاهیم اصلی رگرسیون لجستیک را دوره کنیم.
رگرسیون لجستیک
در مقالهی دیگری (رگرسیون لجستیک)، برخی از جنبههای رگرسیون لجستیک را مطرح کردیم. اجازه دهید مجدداً از تصویری از همان مقاله استفاده کنم. پیشنهاد میکنم آن مقاله را بخوانید، چرا که برای درک برخی از مفاهیم مطرحشده در اینجا مفید خواهند بود.
در مورد ما، z تابعی از سن است؛ احتمال وام بد را بهصورت زیر تعریف میکنیم: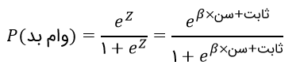
تأثیر ثابت ایلر روی رگرسیون لجستیک را باید متوجه شده باشید. احتمال بد بودن وام وقتی z یه سمت منفی بینهایت می رود برابر با 0 و وقتی به سمت مثبت بینهایت می رود برابر با 1 میشود. این امر کرانهای احتمال را در ۰ و ۱، در هر دو طرف بینهایت حفظ میکند.
بهعلاوه، میدانیم که احتمال وام خوب، یک منهای احتمال وام بد است، پس:![]()
اگر تابهحال در هر نوع شرطبندیای شرکت کرده باشید، میدانید که شرطها باتوجه به شانس بسته میشوند. از لحاظ ریاضی، شانس، احتمال بُرد تقسیم بر احتمال باخت است. اگر شانس مسئلهمان را حساب کنیم، معادلهی زیر بهدست میآید. 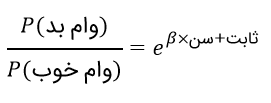
در اینجا، ثابت ایلر با ابهت تمام مشخص است.
طبقهبندی نادقیق
حالا، بیایید دستههای نادقیقی از مجموعهدادهای که در مقالهی اول این سری دیدیم برای گروههای سنی بسازیم. دستههای نادقیق بهواسطهی تلفیق گروههایی که ضمن حفظ روند کلی نرخهای بد، نرخهای بد مشابهی دارند شکل میگیرند. همین کار را برای گروههای سنی هم انجام میدهیم: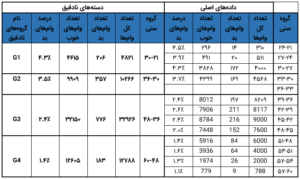
از چهار دستهی نادقیق بالا برای اجرای الگوریتم رگرسیون لجستیک استفاده خواهیم کرد. همانطور که در مقالهی قبلی دایکه گفتیم، الگوریتم میکوشد Z را بهینه کند. در مورد ما، Z ترکیبی خطی از گروه سنی است، یعنی ثابت + G3 + G2 + G1 = Z. همانطور که متوجه شدید در این معادله از G4 استفاده نکردیم. چرا که این ثابت اطلاعات G4 را جذب خواهد کرد. این شبیه استفاده از متغیرهای ساختگی در رگرسیون خطی است. اگر میخواهید جزئیات بیشتری راجع به این موضوع یاد بگیرید، میتوانید سؤالتان را روی همین وبلاگ مطرح کنید تا بیشتر راجع به آن بحث کنیم.
رگرسیون لجستیک
حالا، آمادهایم تا رگرسیون لجستیک نهاییمان را ازطریق برنامهی آماری برای معادلهی زیر بسازیم:
بدین منظور، میتوانید یا از نرمافزار تجاری (SAS، SPSS یا مینیتب) یا از نرمافزار آزاد (R) استفاده کنید. همهی این نرمافزارها جدولی شبیه جدول زیر میسازند: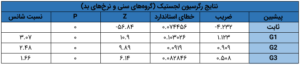
اجازه دهید سریعاً این جدول را رمزگشایی کنیم و نحوهی برآورد ضرایبی در اینجا را بفهمیم. بیایید به ستون آخر این جدول، یعنی نسبت شانس، نگاهی بیندازیم. نرمافزار چطور به مقدار ۳.۰۷ برای G1 رسید؟ شانس (وامهای خوب/ بد) G1، ۴.۴۶ درصد = ۴۶۱۵/۲۰۶ است. نسبت شانس، نسبت این دو عدد است، یعنی ۳.۰۷ = ۱.۴۵٪/۴.۴۶٪. حالا، لگاریتم طبیعی ۳.۰۷ را بگیرید، یعنی ۱.۱۲۳ = (۳.۰۷)In – این c ما برای G1 است. به همین ترتیب، میتوانید ضریب G2 و G3 را هم بیابید. با ماشین حسابتان امتحان کنید!
این ضرایب، مقادیر β در معادلهی اولیه هستند و بنابراین، معادله بهصورت زیر درخواهد آمد: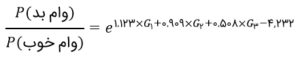
حواستان باشد که فقط مقادیر ۱ یا ۰ را میتوان به G1، G2 و G3 داد. بهعلاوه، از آنجاییکه G1، G2 و G3 دوبهدوناسازگارند، پس وقتی یکی از آنها ۱ باشد، بقیه خودبهخود ۰ میشوند. اگر G1 را ۱ بگیرید، معادله بهصورت زیر درمیآید: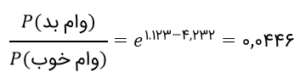
به همین ترتیب، میتوانیم مقدار برآوردشدهی نرخ بد برای G1 را هم پیدا کنیم: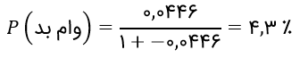
این دقیقاً همان مقداریست که مشاهده کردیم. پس، رگرسیون لجستیک در برآورد نرخ بد بهخوبی کارساز است. ای ول! اولین مدلمان را ساختیم.
مخلص کلام
ایلر گرچه نابینا بود، اما راه رسیدن تا اینجا را به ما نشان داد! اجازه دهید حقایق بیشتری راجع به زیباترین فرمول جهان که در سرآغاز همین مقاله بحث کردیم، فاش کنم. بین پنج مقام برتر، دو فرمول دیگر هم میبینید که توسط لئونهارد ایلر کشف شدند. این یعنی ۳ فرمول از ۵ تا از زیباترین فرمولهای جهان. واو! فکر کنم باید نابینا را بازتعریف کنیم.
[1] Leonhard Euler